свойство Матрица преобразованийCSS3-генератор ☛

Матрица преобразований предназначена для вычисления новых координат элемента с целью его трансформации и позволяет установить множество преобразований одновременно. Различают двумерную и трёхмерную матрицу, они отличаются друг от друга размером и пространством, на которое ориентированы. Поскольку двумерная матрица по размеру меньше и поэтому проще, на её примере рассмотрим общий принцип работы матриц.

Двумерная матрица

Преобразование с помощью двумерной матрицы происходит в плоскости экрана, при этом соблюдается условие, что линии всегда остаются параллельными, поэтому в качестве трансформации допустимы поворот, масштабирование, наклон и изменение положения, но никак не перспектива или нечто подобное. Это уже область работы трёхмерной матрицы. На рис. 1 показаны допустимые и невозможные преобразования, выполненные с помощью двумерных матриц.

Исходный элементПоворотНаклонА вот так сделать нельзя
Исходный элементПоворотНаклонА вот так сделать нельзя

Рис. 1. Трансформация элемента

Сама матрица имеет размер 3х3 и в общем виде записывается так:

Матрица преобразований

Иногда для простоты третью строку опускают, поскольку она не оказывает влияния на конечный результат. Новые координаты каждой точки элемента получаются путём умножения матрицы преобразований на матрицу координат.

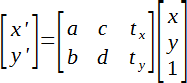
Умножение матриц

И вычисляются по следующей формуле:

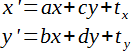
Формула преобразования

Роль каждого коэффициента матрицы представлена в табл. 1.

Табл. 1. Коэффициенты матрицы преобразований
КоэффициентПреобразованиеОписание
aИзменение размера по горизонталиИзменение масштаба по горизонтали. Значение больше 1 расширяет элемент, меньше 1, наоборот, сжимает.
bНаклон по горизонталиНаклон по вертикали. Положительное значение наклоняет вверх, отрицательное вниз.
cНаклон по вертикалиНаклон по горизонтали. Положительное значение наклоняет влево, отрицательное вправо.
dИзменение размера по вертикалиИзменение масштаба по вертикали. Значение больше 1 расширяет элемент, меньше 1 — сжимает.
txСмещение по горизонтали в пикселяхСмещение по горизонтали в пикселях. Положительное значение сдвигает элемент вправо на заданное число пикселей, отрицательное значение сдвигает влево.
tyСмещение по вертикали в пикселяхСмещение по вертикали в пикселях. При положительном значении элемент опускается на заданное число пикселей вниз или вверх при отрицательном значении.

Для матрицы преобразований применяется функция matrix(), внутри скобок перечисляются коэффициенты.

transform: matrix(a, b, c, d, tx, ty)

Единичная матрица

Если в матрице коэффициенты a и d равны 1, а остальные элементы матрицы нулевые, то такая матрица называется единичной. Эта матрица применяется по умолчанию, поскольку не приводит к какой-либо трансформации элемента. Так что если необходимо произвести только один вид преобразований, единичную матрицу надо брать в качестве основы.

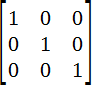
Единичная матрица

Масштаб по горизонтали

Чтобы увеличить размер элемента, допустим, в два раза по горизонтали, коэффициент a следует установить равным 2, а остальные коэффициенты оставить как в единичной матрице.

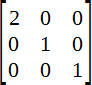
Масштабирование

Считаем новые координаты:

x' = 2*x + 0*y + 0
y' = 0*x + 1*y + 0

И окончательно:

x' = 2x
y' = y

Код для масштабирования показан в примере 1.

Пример 1. Масштабирование
<!DOCTYPE html>
<html>
 <head>
  <meta charset="utf-8">
  <title>Трансформация</title>
  <style>
   .t {
    background: #e7685d; /* Цвет фона */
	color: #fff; /* Цвет текста */
    padding: 10px; /* Поля */
    width: 300px; /* Ширина */
	transform-origin: 0 0; /* Точка трансформации */
    transform: matrix(1.2, 0, 0, 1, 0, 0); /* Трансформация */
   }
  </style>
 </head>
 <body>
  <div class="t">
   <p>То, что делает армию при встрече с противником непобедимой, 
      это правильный бой и маневр.</p>
   <p>Сунь-Цзы. Искусство войны. Пер. Н. Конрад.</p>
  </div>
 </body>
</html>

Результат данного примера показан на рис. 2. Блок с текстом растягивается на 20% по горизонтали.

Изменение масштаба текста

Рис. 2. Изменение масштаба текста

Отражение

Для отражение элемента по горизонтали следует установить a=-1, по вертикали d=-1 или оба значения одновременно для отражения одним разом по горизонтали и вертикали.

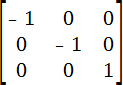
Отражение

В примере 2 показано отражение текста по вертикали.

Пример 2. Отражение
<!DOCTYPE html>
<html>
 <head>
  <meta charset="utf-8">
  <title>Трансформация</title>
  <style>
   .t {
    transform: matrix(1, 0, 0, -1, 0, 0);
   }
  </style>
 </head>
 <body>
  <p class="t">Через миг Алиса прошла сквозь зеркало 
   и легко спрыгнула в Зазеркалье.</p>
 </body>
</html>

Результат данного примера показан на рис. 3.

Отражение текста по вертикали

Рис. 3. Отражение текста по вертикали

Наклон

За наклон отвечают коэффициенты b и c, которые и влияют на вид элемента. Давайте установим c=1 и посмотрим, какие преобразования получатся.

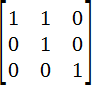
Наклон

x' = 1*x + 1*y + 0
y' = 0*x + 1*y + 0

x' = x + y
y' = y

Таким образом, меняется только координата x, которая увеличивается на значение y, что и приводит к наклону элемента. В примере 3 используется отрицательное значение коэффициента c для наклона вправо.

Пример 3. Наклон
<!DOCTYPE html>
<html>
 <head>
  <meta charset="utf-8">
  <title>Трансформация</title>
  <style>
   .t {
    background: #e7685d; /* Цвет фона */
	color: #fff; /* Цвет текста */
    padding: 10px; /* Поля */
    width: 300px; /* Ширина */
	transform-origin: 0 100%; /* Точка трансформации */
    transform: matrix(1, 0, -0.5, 1, 0, 0); /* Трансформация */
   }
  </style>
 </head>
 <body>
  <div class="t">
   <p>То, что делает армию при встрече с противником непобедимой, 
   это правильный бой и маневр.</p>
   <p>Сунь-Цзы. Искусство войны. Пер. Н. Конрад.</p>
  </div>
 </body>
</html>

Результат данного примера показан на рис. 4.

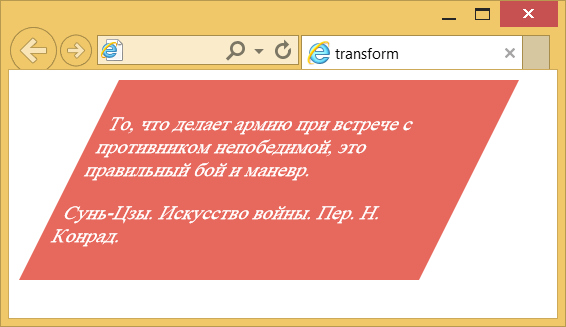
Наклон блока

Рис. 4. Наклон блока

Поворот

Поворот является комбинацией масштабирования и наклона, но чтобы сохранить исходные пропорции элемента преобразования должны подчиняться строгим вычислениям с использование синусов и косинусов.

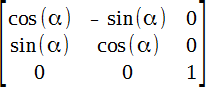
Поворот

Сам поворот происходит по часовой стрелке, α задаёт угол поворота в градусах.

Перемещение

За сдвиг элемента по горизонтали отвечает коэффициент tx, а по вертикали ty. Значением выступает число пикселей.

Трёхмерная матрица

Трёхмерная матрица имеет размер 4х4 и применяется для преобразования координат элемента в трёхмерном пространстве. В общем виде она выглядит так:

Трёхмерная матрица

Название «трёхмерная» лишь отражает тот факт, что матрица предназначена для работы в 3d-пространстве. Двумерная матрица является её частным случаем и для размера 4х4 имеет следующий вид:

В чистом виде эта матрица применяется редко из-за своей сложности и наличия удобных функций для трансформации в пространстве. Если вам интересна тригонометрия и формулы преобразований одних координат в другие, то почитайте этот материал.

https://developer.mozilla.org/en-US/docs/Web/CSS/transform-function

Справочник CSS⌕≡
×
Справочник CSS